How Much Insulation Do I Need for a 10x16 Shed?

The amount of insulation that you need for 10×16 shed depends on things like the roof design, stud size, and stud spacings. Because of this, the amount can vary.

The following provides you with a detailed step-by-step breakdown of how to calculate the amount of insulation needed for the walls and roof of the shed.

However, if you are not interested in the calculations, then skip to the last section. There you will find tables for the amount of insulation needed for 10×16 sheds with specific roof designs, stud sizes, and stud spacings.

To insulate a 10×16 shed, approximately 477.01 ft2 to 532.37 ft2 of insulation is needed, depending on the stud size, stud spacing, and roof design.

Contents show table of contents

Calculating Actual Wall Area Requiring Insulation

Ceiling Height Must Be Considered

You can measure your exact ceiling height and make adjustments to the calculations presented below, but we are going to work based on the fact that the shed has a standard ceiling height of 8 ft.

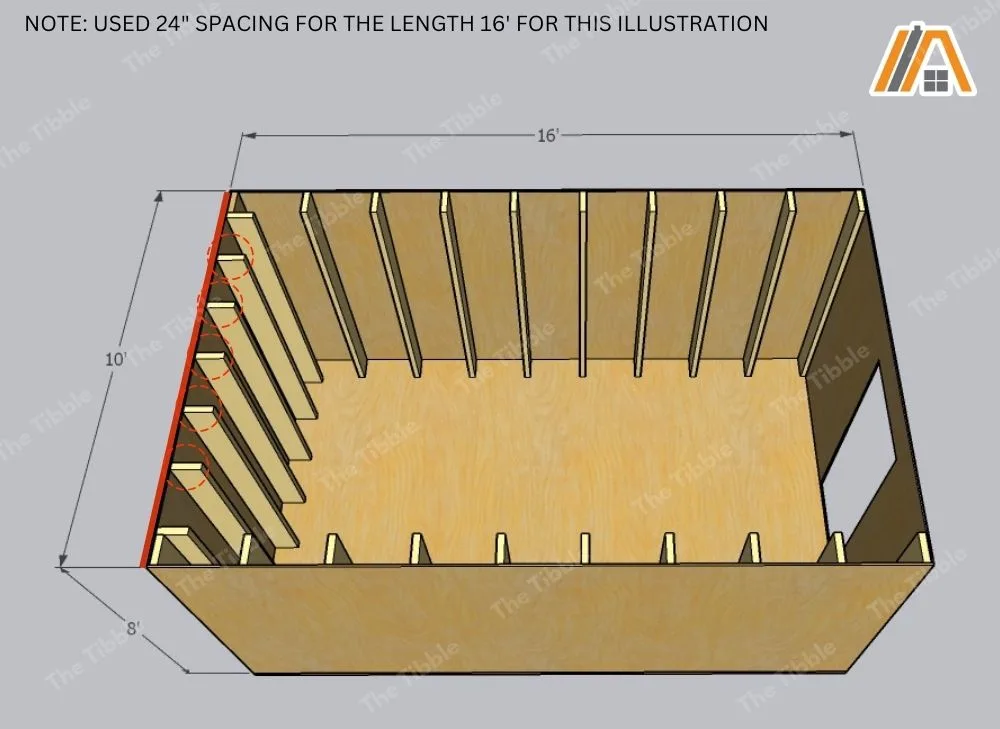
Understanding the 10×16 Measurements

The 10×16 measurements are the outside measurements of the shed. The inside measurements need to be adjusted for the presence of stud work.

We will be calculating the internal measurements. We will not be accounting for doors and windows. The areas of these are easy to calculate, so you can add up the total area taken up by these, depending on the number and location and subtract this from the total area.

Stud Sizes

Along each 16-ft wall, you are going to lose 2 in. at each end for the first and last studs. This cuts the insulation area from 128 ft² (16 ft x 8 ft) to 125.33 ft² according to the following:

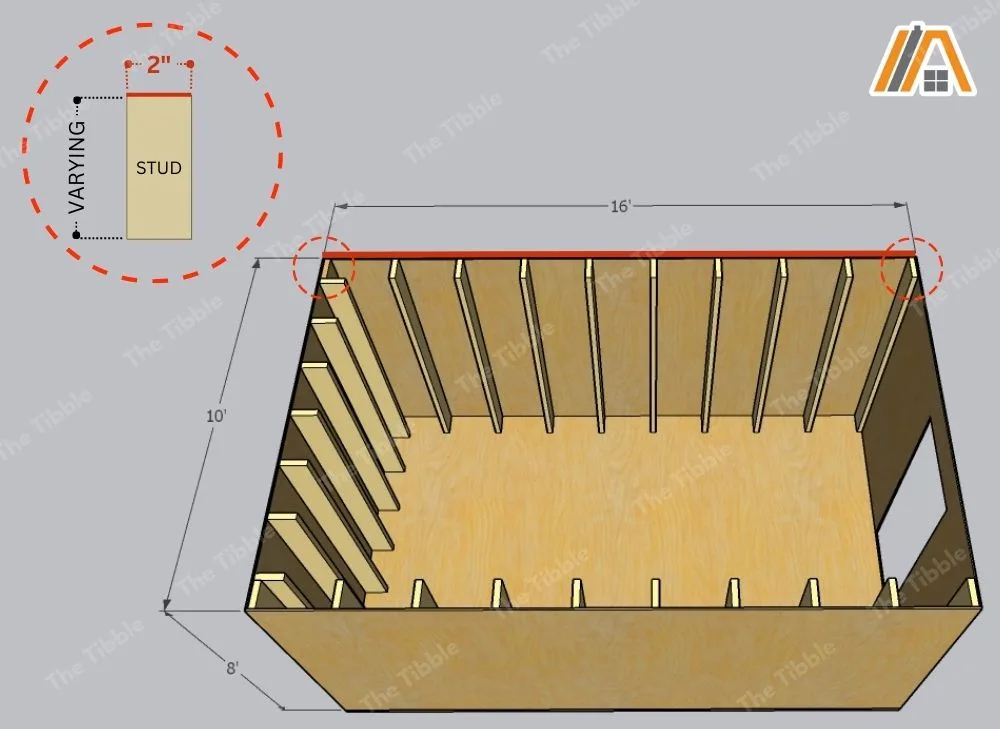
Studs on the ends of long span wall of a 10 foot by 16 foot shed

Calculation (1a): 16 ft x 12 = 192 in.

Calculation (1b): 192 in. – (2 + 2) in = 188 in.

Calculation (1c): 188 in. /12 = 15.67 ft

Calculation (1d): 15.67 ft x 8 ft = 125.33 ft²

Along each 10-ft wall, you are also going to lose 2 in. at each end for the first and last studs. This cuts the insulation area from 80 ft² (10 ft x 8 ft) to 77.33 ft² according to the following:

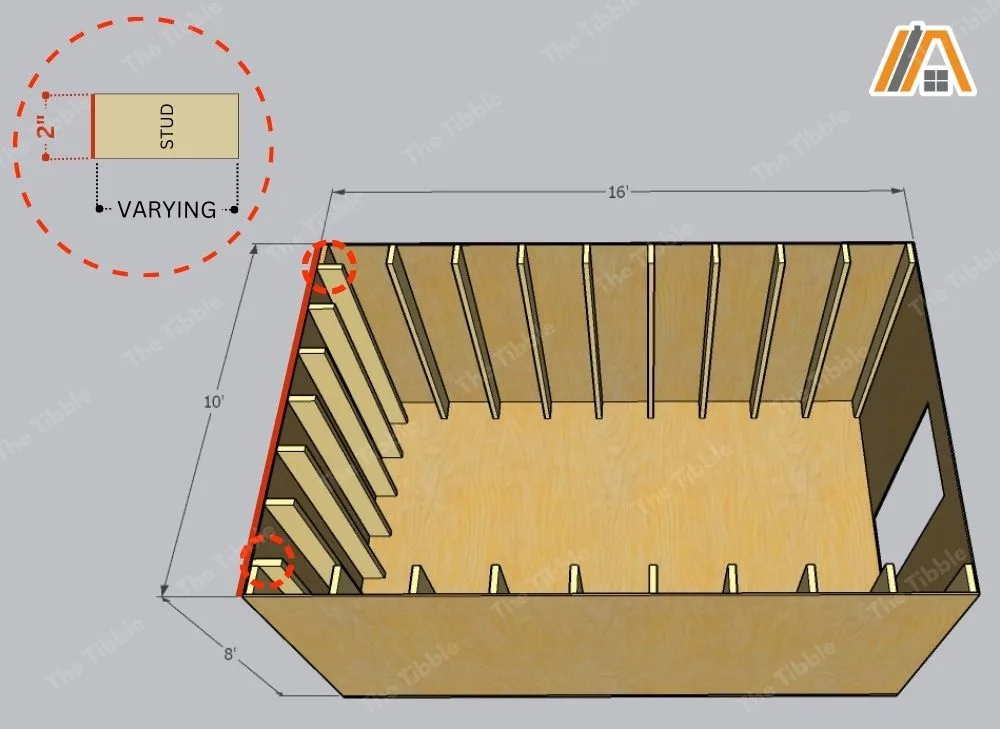
Studs on the end of the short span wall in a 10 foot by 16 foot shed

Calculation (2a): 10 ft x 12 = 120 in.

Calculation (2b): 120 in. – (2 + 2) in = 116 in.

Calculation (2c): 116 in. /12 = 9.67 ft

Calculation (2d): 9.67 ft x 8 ft = 77.33 ft²

In addition, you will lose the depth of one stud at each end. This accounts for the end studs of the long walls. The amount of space lost here depends on the size of the studs you use.

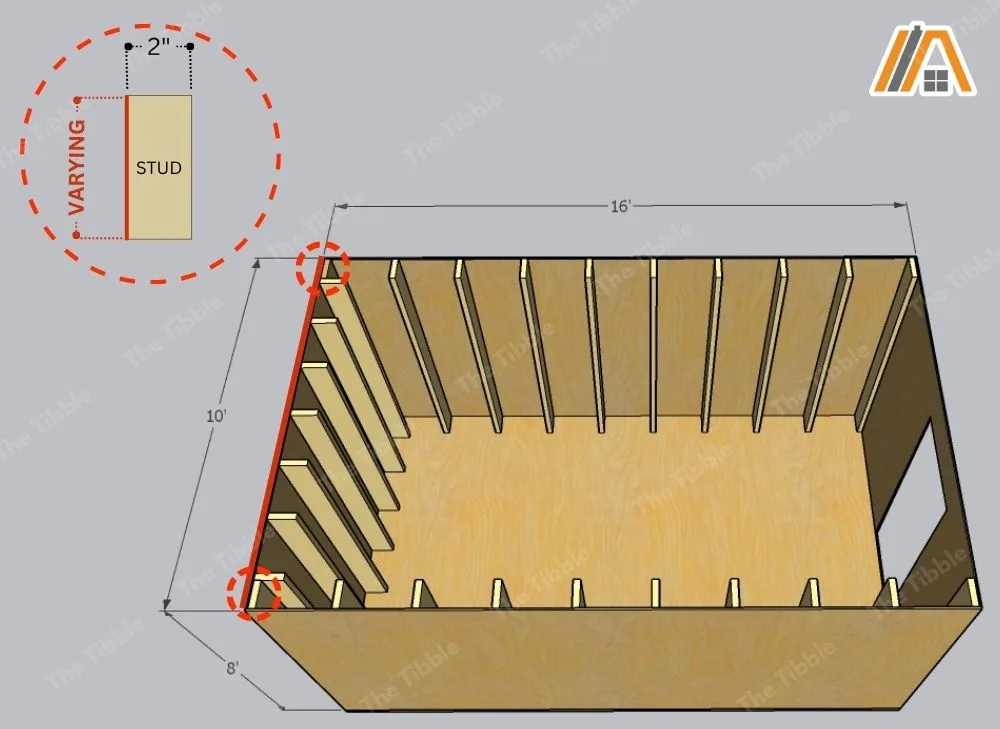
Studs on the end of long span wall occupying space along the short span of a 10 foot by 16 foot shed

I imagine that for a shed, you’ve probably used 2×4, 2×6, or 2×8 studs. Anything larger and you lose too much space, particularly considering that there is no minimum insulation thickness/R-value requirements for a shed.

2×4, 2×6, or 2×8 studs means a loss of 8 in., 12 in., or 16 in., respectively.

Let’s plug these figures in the above equations. We will deduct them from the length in inches (given in Calculation (2b)).

For each 10-foot wall:

	New length	New length in feet	New area
2×4 studs	116 in. – 8 in. = 108 in.	180 in. /12 = 9 ft	9 ft x 8 ft = 72 ft2
2×6 studs	116 in. – 12 in. = 104 in.	104 in. /12 = 8.67 ft	8.67 ft x 8 ft = 69.33 ft2
2×8 studs	116 in. – 16 in. = 100 in.	100 in. /12 = 8.33 ft	8.33 ft x 8 ft = 66.67 ft2

Table 1

Stud Spacing

Then, of course, you must deduct the area used up by the rest of the studs along the wall. This depends on the number of studs used, and the number of studs used depends on the stud spacing chosen.

The recommended stud spacing for a shed wall is 16-24 in.

We’re going to look at the length available between the two end studs. So, for each 16-ft wall, this is 188 in. (Calculations (1b)) and for each 10-ft wall, it is 108 in., 104 in., and 100 in., depending on the stud size (Table 1).

For each 16-ft wall:

16 in. stud spacing	18 in. stud spacing	20 in. stud spacing	22 in. stud spacing	24 in. stud spacing
11.75 studs	10.44 studs	9.4 studs	8.55 studs	7.83 studs
In real life, you would use 11 studs	In real life, you would use 10 studs	In real life, you would use 9 studs	In real life, you would use 9 studs	In real life, you would use 8 studs

Table 2

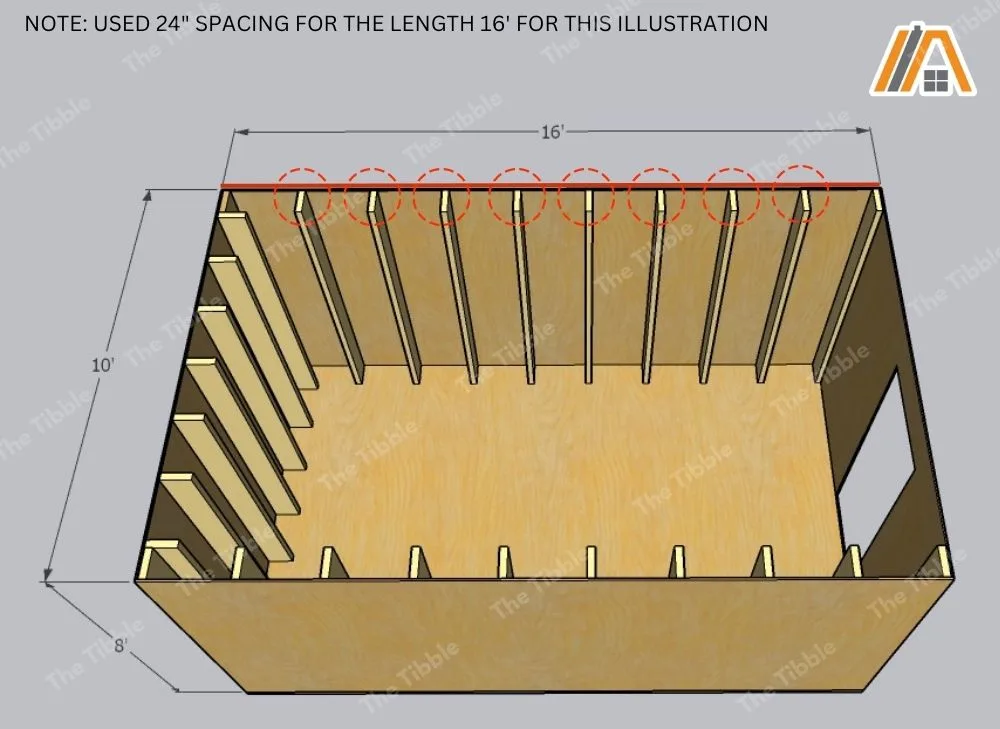
Number of studs placed in the long span 16 feet wall of a shed

For each 10 ft wall:

	16 in. stud spacing	18 in. stud spacing	20 in. stud spacing	22 in. stud spacing	24 in. stud spacing
2×4 studs	6.75 studs (in real life, you would use 6 studs)	6 studs	5.4 studs (in real life, you would use 5 studs)	4.9 studs (in real life, you would use 5 studs)	4.5 studs (in real life, you would use 5 studs)
2×6 studs	6.5 studs (in real life, you would use 6 studs)	5.78 studs (in real life, you would use 5 studs)	5.2 studs (in real life, you would use 5 studs)	4.73 studs (in real life, you would use 5 studs)	4.33 studs (in real life, you would use 5 studs)
2×8 studs	6.25 studs (in real life, you would use 6 studs)	5.56 studs (in real life, you would use 5 studs)	5 studs	4.55 studs (in real life, you would use 5 studs)	4.17 studs (in real life, you would use 5 studs)

Table 3

Number of studs placed in the short span 10 feet wall of a shed

Total Wall Area to Cover

For each additional stud, you are going to subtract 2 in. from the total wall width. Multiplying this by the height will give you the total wall area needed to be covered by insulation.

For the 16-ft walls:

	Width excluding studs	Area requiring insulation (per wall)	Area requiring insulation (both walls)
11 studs	166 in. = 13.83 ft	110.67 ft²	221.34 ft²
10 studs	168 in. = 14 ft	112 ft²	224 ft²
9 studs	170 in. = 14.17 ft	113.33 ft²	226.66 ft²
8 studs	172 in. = 14.33 ft	114.67 ft²	229.34 ft²

Table 4

For the 10-ft walls:

	Width excluding studs	Area requiring insulation (per wall)	Area requiring insulation (both walls)
6 studs	2×4: 96 in. = 8 ft 2×6: 92 in. = 7.67 ft 2×8: 88 in. = 7.33 ft	2×4: 64 ft² 2×6: 61.33 ft² 2×8: 58.67 ft²	2×4: 128 ft² 2×6: 122.66 ft² 2×8: 117.34 ft²
5 studs	2×4: 98 in. = 8.17 ft 2×6: 94 in. = 7.83 ft 2×8: 90 in. = 7.5 ft	2×4: 65.33 ft² 2×6: 62.67 ft² 2×8: 60 ft²	2×4: 130.66 ft² 2×6: 125.34 ft² 2×8: 120 ft²

Table 5

For the walls in total:

Stud spacing	2×4 studs	2×6 studs	2×8 studs
16 in.	221.34 ft² + 128 ft² = 349.34 ft²	221.34 ft² + 122.66 ft² = 344 ft²	221.34 ft² + 117.34 ft² = 338.68 ft²
18 in.	224 ft² + 128 ft² = 352 ft²	224 ft² + 125.34 ft² = 349.34 ft²	224 ft² + 120 ft² = 344 ft²
20 in.	226.66 ft² + 130.66 ft² = 357.32 ft²	226.66 ft² + 125.34 ft² = 352 ft²	226.66 ft² + 120 ft² = 346.66 ft²
22 in.	226.66 ft² + 130.66 ft² = 357.32 ft²	226.66 ft² + 125.34 ft² = 352 ft²	226.66 ft² + 120 ft² = 346.66 ft²
24 in.	229.34 ft² + 130.66 ft² = 360 ft²	229.34 ft² + 125.34 ft² = 354.68 ft²	229.34 ft² + 120 ft² = 349.34 ft²

Table 6

Calculating Actual Roof Area Requiring Insulation

For the roof, you also have to calculate the area minus the rafters.

However, things can get a little complicated because you have to take into account the roof design (gable, skillion, or flat). If you have a skillion or gable roof, the pitch adds additional area.

Flat Roofs

The area of the flat roof without rafters is going to be:

Calculation (3a): 10 ft x 16 ft = 160 ft²

However, you will be installing rafters, so we need to deduct the widths of these—insulation is only installed between the rafters.

Each rafter is 2 in. wide, installed parallel to the short edge (if you stood at the short end, you would see them crossing left to right), and the recommended rafter spacing for sheds is 16 in.

This means that we are looking at a starting width of:

Calculation (3b): 16 ft x 12 = 192 in.

Let’s deduct the width of the two end rafters as these have to be at the end and the rest of the rafters will be spaced between them.

Calculation (3c): 192 in. – 4 in. = 188 in.

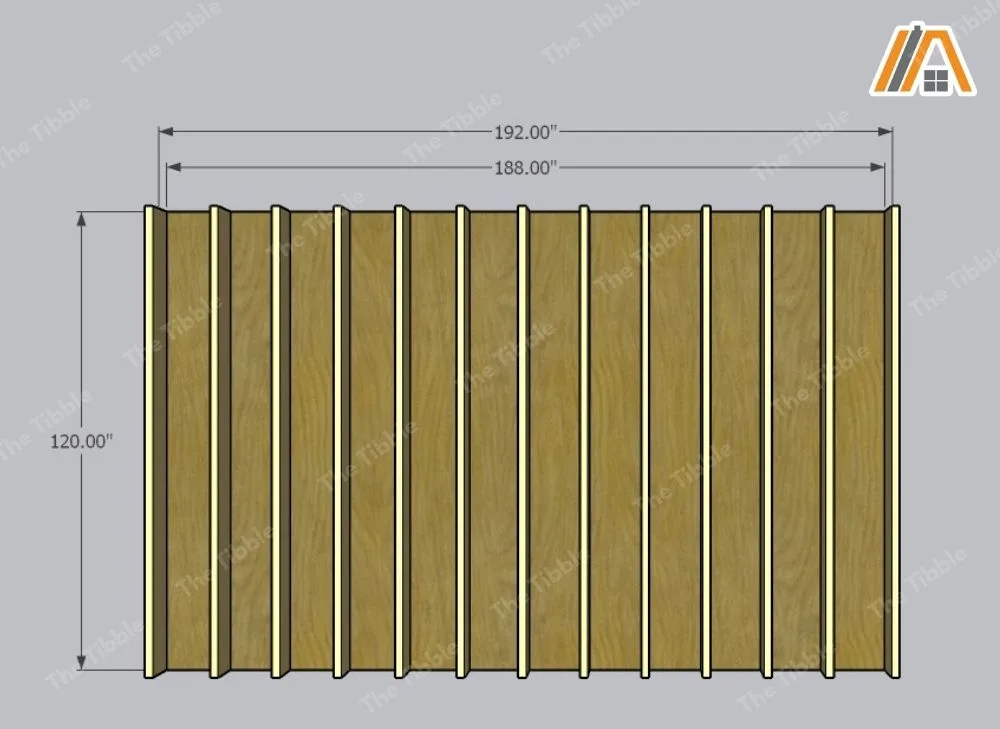
Rafter dimensions of a 10x16 shed for a flat roof

With a recommended spacing of 16 in., you will need 11.75 rafters (Table 2). Now, you can’t have a fraction of a rafter, so we’re going to round this down to 11 rafters.

You can round up to 12 if you choose, particularly if you are opting for a heavier roofing material, but 11 rafters should be sufficient in most cases.

Eleven rafters between the two end ones means an additional loss of:

Calculation (3d): 11 x 2 in. = 22 in.

Using this, we can calculate the area that insulation will be required to cover a flat roof for a 10×16 shed:

Calculation (4a): 188 in. – 22 in. = 166 in.

Calculation (4b): 166 in. /12 = 13.83 ft

Calculation (4c): 13.83 ft x 10 ft = 138.33 ft²

Gable Roofs

Roof Panels

The first thing that we have to look at here is the pitch. The minimum pitch you need is a 1/4 in. increase in rise (the distance from the ceiling line to the roof) for every foot of run (the distance from the edge of the building to the center of it).

However, this pitch means an angle of only 1.19°, which is unlikely to be the pitch you choose for your gable-roofed shed.

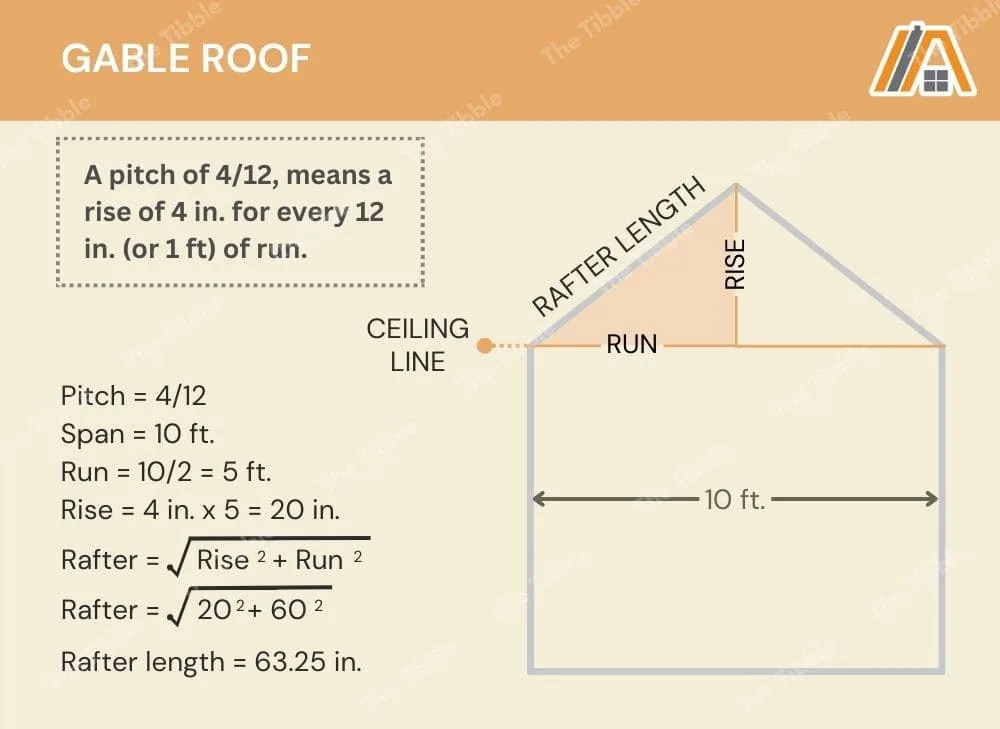
Formula for rafter length, rise and run of a 10x16 shed with a gable roof

Instead, we will look at a pitch of 4/12, which means a rise of 4 in. for every 12 in. (or 1 ft) of run. This seems to be a common pitch used for gable-roofed sheds.

For a 10×16 shed, the run is:

Calculation (5a): 10 ft /2 = 5 ft

So, there are 5 x 1 ft lengths, which means the rise is calculated to be:

Calculation (5b): 4 in. x 5 = 20 in.

Using pythagoras’ theorem, we can use this to calculate the rafter length (represented as the hypotenuse).

Calculation (6a): Hypotenuse = √(adjacent)2 + (opposite)2

Calculation (6b): C = √(A)2 + (B)2

Calculation (6c): C = √(20)2 + (60)2

Calculation (6d): C = √400 + 3600

Calculation (6e): C = √4000

Calculation (6f): C = 63.25 in.

The rafter length up each side of the roof is, therefore, 63.25 in. or 5.27 ft.

The rafter spacing that is used for flat roofs is also used for gabled roofs. So, each side has 2 + 11 rafters, each with a width of 2 in.

We have already done this calculation in the section on flat roofs (Calculation (4b)). The roof width less the width of the rafters is 13.83 ft.

Thus, the area of each side that needs to be covered in insulation is:

Calculation (7a): 5.27 ft x 13.83 ft = 72.88 ft²

And the total area of the roof panels that required insulation covering is:

Calculation (7b): 72.88 ft² x 2 = 145.76 ft²

Gable Spaces

As the roof has a peak, there are two triangles of space between the short walls and the apex of the roof. These spaces also needs to be insulated.

The space is reduced by the broad side of the rafters on each side of the peak, the broad side of a rafter set along the top of the wall (as if you were laying the first joist for a ceiling), and at least one upright beam that is set with the broad side out and which bisects the triangle.

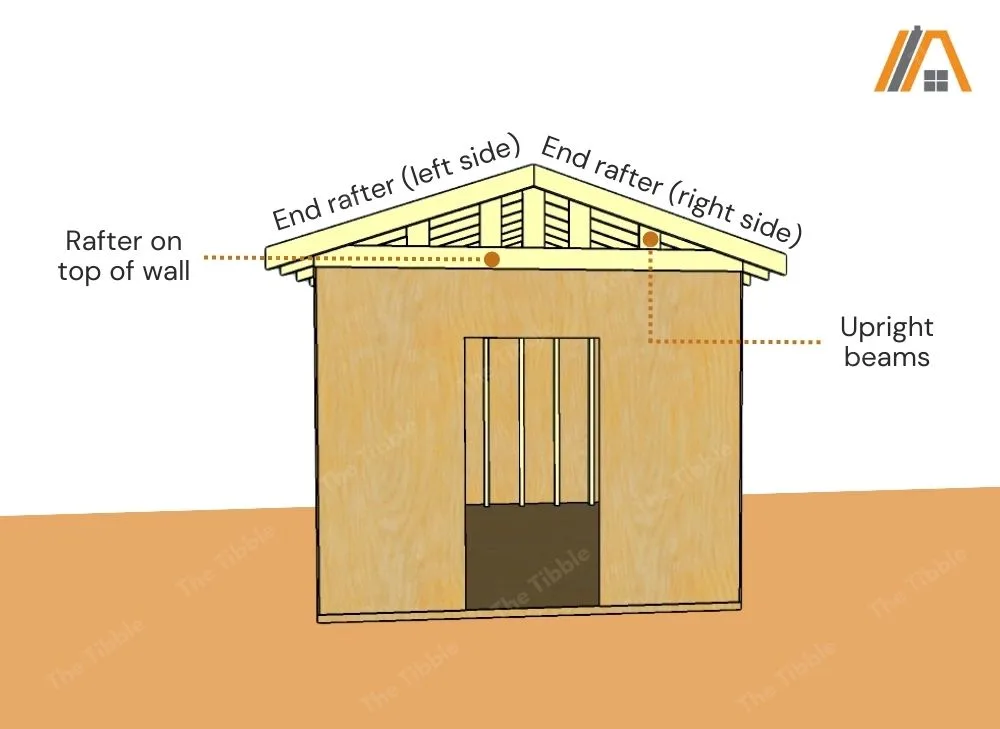
Rafter parts of a 10x16 shed with a gable roof

Because all of these beams are facing broad side out, the size of the beams comes into play.

You will most likely use 2×4 or 2×6 rafters.

The rise of 20 in. (Calculation (5b)) is reduced by:

8 in. at the top and bottom for 2×4 rafters
12 in. at the top and bottom for 2×6 rafters

This means that the rise of the space is:

12 in. if you are using 2×4 rafters
8 in. if you are using 2×6 rafters

While the rafters reduce the internal area of the triangular gable space, because they are all either 2×4 or 2×6, it does not alter the angles. (Triangles are great like that).

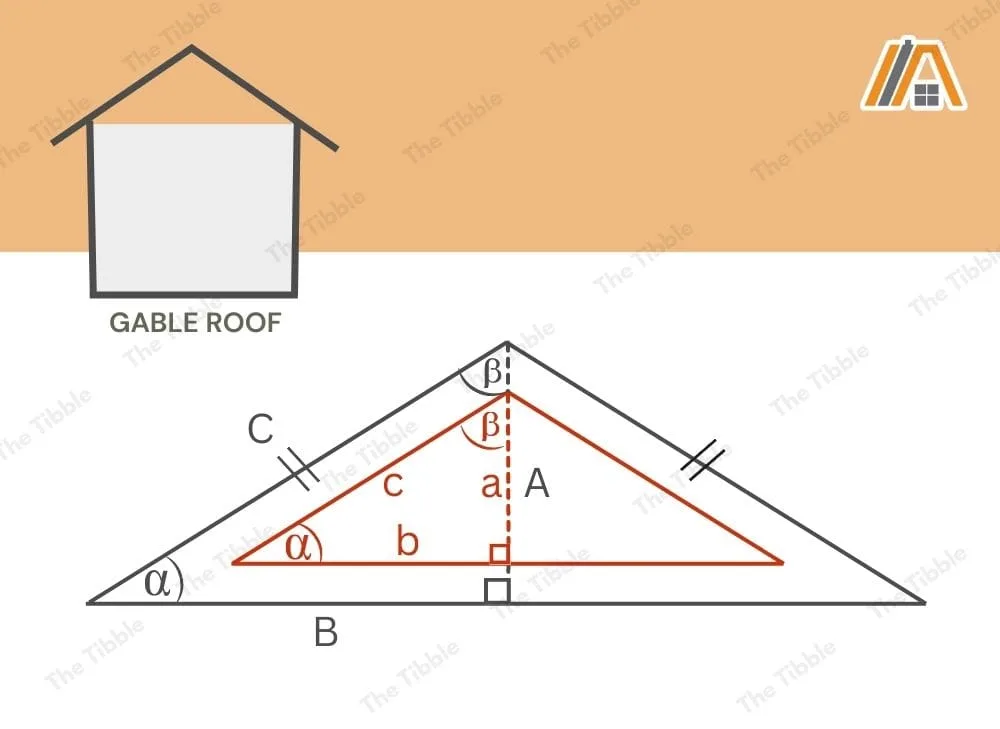
To calculate the area of these gable triangles, we need to know the values of a and b in the above diagram.

Here’s what we know:

A = 20 in. (Calculation (5b))
B = 5 ft = 60 in. (Calculation (5a))
C = 63.25 in. (Calculation (6f))

We can calculate α using trigonometry:

Calculation (8a): sin(α) = opposite/hypotenuse

Calculation (8b): sin(α) = A/C

Calculation (8c): sin(α) = 20/63.25

Calculation (8d): sin(α) = 0.316205533

Calculation (8e): α = sin^-1(0.316205533)

Calculation (8f): α = 18.43°

As stated previously, the angles of the larger triangle are the same for the smaller one.

To calculate the length of a, we need to subtract the top and bottom rafter dimensions.

I want to note here that this is not a fully accurate measurement because the center parallel beam means that we are not actually measuring through the proper central point.

However, once we have completed the rest of the calculations, I find it makes minimal difference.

So, for 2×4 rafters:

Calculation (9a): a = A – (2 x 4 in.)

Calculation (9b): a = 20 in. – 8 in.

Calculation (9c): a = 12 in.

And for 2×6 rafters:

Calculation (10a): a = A – (2 x 6 in.)

Calculation (10b): a = 20 in. – 12 in.

Calculation (10c): a = 8 in.

The area of a triangle is calculated as (base x height)/2. Base is b and height is a. We know a, so we need to calculate b. We are going to do this using more trigonometry.

For 2×4 rafters:

Calculation (11a): tan (α) = opposite/adjacent

Calculation (11b): tan (α) = a/b

Calculation (11c): tan (α) = 12/b

Calculation (11d): tan (18.43) = 12/b

Calculation (11e): 0.333237365 = 12/b

Calculation (11f): b = 12/0.333237365

Calculation (11g): b = 36.01 in.

From b, we are going to subtract half the parallel beam:

Calculation (11h): b = 36.01 in. – 2 in.

Calculation (11i): b = 34.01 in.

For 2×6 rafters:

Calculation (12a): tan (α) = opposite/adjacent

Calculation (12b): tan (α) = a/b

Calculation (12c): tan (α) = 8/b

Calculation (12d): tan (18.43) = 8/b

Calculation (12e): 0.333237365 = 8/b

Calculation (12f): b = 8/0.333237365

Calculation (12g): b = 24.01 in.

Again, we adjust for the central beam:

Calculation (12h): b = 24.01 in. – 3 in.

Calculation (12i): b = 21.01 in.

Now we can calculate the area of the triangles.

Remember that this is only for one side of the central parallel beam, so we need to double it at the end. Since the final step is to divide by two, we can essentially skip this step, but I will include it anyway.

Then, we have to double the number again for the opposite gable.

	2×4 rafters	2×6 rafters
Area of half the gable	(base x height) /2	(base x height) /2
	(b x a) /2	(b x a) /2
	(34.01 in. x 12 in.) /2	(21.01 in. x 8 in.) /2
	408.12 in.² /2	168.08 in.² /2
	204.06 in.²	84.04 in.²
Area of one gable	204.06 in.² x 2	84.04 in.² x 2
	408.12 in.²	168.08 in.²
Area of one gable in ft²	2.83 ft²	1.17 ft²
Total gable area	2.83 ft² x 2	1.17 ft² x 2
	5.66 ft²	2.34 ft²

Table 7

Total Gable Roof Area Requiring Insulation

	2×4 rafters	2×6 rafters
Roof panels	145.76 ft²	145.76 ft²
Gable spaces	5.66 ft²	2.34 ft²
Total area	151.42 ft²	148.1 ft²

Table 8

Skillion Roofs

Roof Panel

Again, we start with pitch. Skillion roofs are not going to be as steeply pitched as gable roofs. A common pitch angle for these shed roofs is 10°, so this is what we will use for the calculations.

You can always insert your actual roof pitch into the equations to calculate the area for your roof if it is not 10°.

We first need to calculate the length of the roof. This is the triangle hypotenuse (C) as illustrated below.

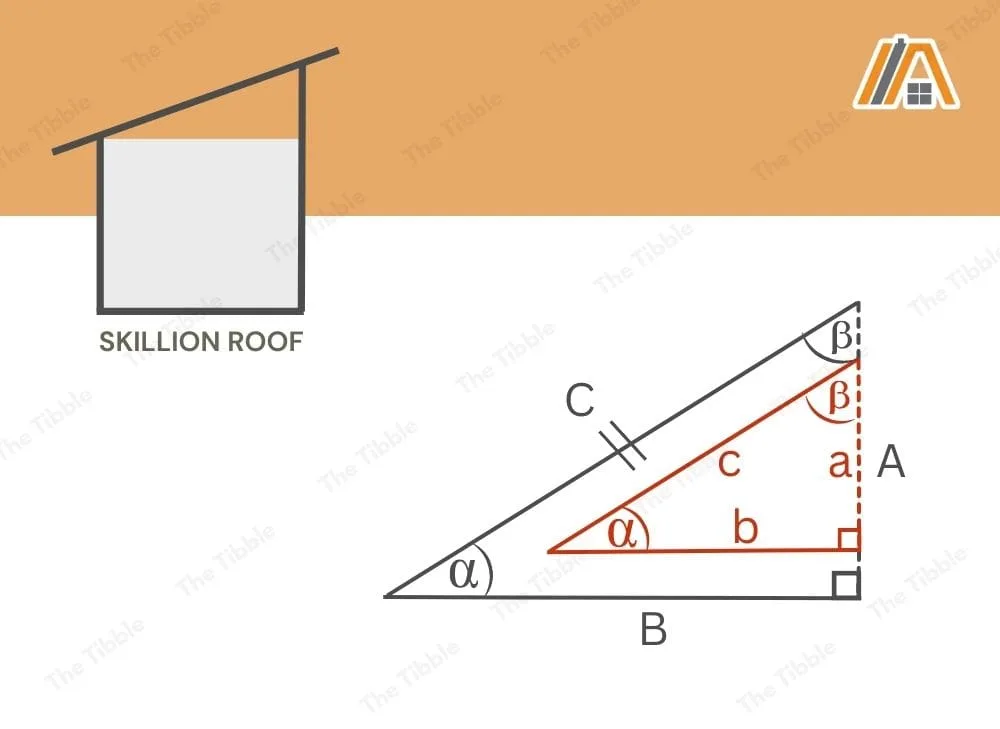
We know the angle α (10°) and the dimension B (10 ft). This means that we can use trigonometry to calculate C.

Calculation (13a): cos(α) = adjacent /hypotenuse

Calculation (13b): cos(α) = B /C

Calculation (13c): cos(10) = 10 ft /C

Calculation (13d): 0.984807753 = 10 ft /C

Calculation (13e): C = 10 ft /0.984807753

Calculation (13f): C = 10.15 ft

Using this and the known width of 16 ft, we can calculate the area of the roof panel without rafters.

Calculation (14a): 10.15 ft x 16 ft = 162.4 ft²

But there are most certainly rafters, so we need to adjust for these.

Each rafter is 2 in. in width. The same spacing applies as before (16 in.). We have actually already calculated the width of the roof minus the the width of the rafters (Calculations (3b), (3c), (3d), (4a), and (4b)).

This width is 13.83 ft. The area of skillion roof panels for a 10×16 shed requiring insulation covering is:

Calculation (14b): 10.15 ft x 13.83 ft = 140.37 ft²

Gable Spaces

Even though this is not a gable roof, there are still those triangles on the side that need to be insulated.

We need to calculate the area of the small triangle in the sketch above. The area is decreased by the broad side of a rafter beam along the edge of the roof panel, the top of the wall at the ceiling line, and the rise.

Again, we can calculate a as A minus the breadth of the beam at the top and bottom of the space. This means it is time to consider the rafter sizes (2×4 and 2×6).

This time, we don’t actually know A, so we need to start here:

Calculation (15a): tan(α) = opposite /adjacent

Calculation (15b): tan(α) = A /B

Calculation (15c): tan(10) = A /10 ft

Calculation (15d): 0.17632698 = A /10 ft

Calculation (15e): A = 10 ft x 0.17632698

Calculation (15f): A = 1.76 ft

Let’s convert this to inches so that we can subtract the rafter breadths (given in inches). 1.76 ft is 21.12 in.

Calculating a for 2×4 rafters:

Calculation (16a): a = A – (2 x 4 in.)

Calculation (16b): a = 21.12 in. – 8 in.

Calculation (16c): a = 13.12 in.

Calculation (16d): 13.12 in. /12 = 1.09 ft

Calculating a for 2×6 rafters:

Calculation (17a): a = A – (2 x 6 in.)

Calculation (17b): a = 21.12 in. – 12 in.

Calculation (17c): a = 9.12 in.

Calculation (17d): 9.12 in. /12 = 0.76 ft

To find the area of the small triangle, we also need to know the base length, which is b.

For 2×4 rafters:

Calculation (18a): tan(α) = opposite /adjacent

Calculation (18b): tan(α) = a /b

Calculation (18c): tan(10) = 1.09 ft /b

Calculation (18d): 0.17632698 = 1.09 ft /b

Calculation (18e): b = 1.09 ft /0.17632698

Calculation (18f): b = 6.18 ft

For 2×6 rafters:

Calculation (19a): tan(α) = opposite /adjacent

Calculation (19b): tan(α) = a /b

Calculation (19c): tan(10) = 0.76 ft /b

Calculation (19d): 0.17632698 = 0.76 ft /b

Calculation (19e): b = 0.76 ft /0.17632698

Calculation (19f): b = 4.31 ft

Now we can calculate the area of one gable space and multiply it by two (to account for the opposite space) to get the total gable area.

	2×4 rafters	2×6 rafters
Area of the gable space	(base x height) /2	(base x height) /2
	(b x a) /2	(b x a) /2
	(6.18 ft x 1.09 ft) /2	(4.31 ft x 0.76 ft) /2
	6.74 ft² /2	3.28 ft² /2
	3.37 ft²	1.64 ft²
Total gable area	3.37 ft² x 2	1.64 ft² x 2
	6.74 ft²	3.28 ft²

Table 9

Wall Extension

We’re not done yet! With skillion roofs, we also have to insulate the side of the roof that is essentially an extension of the one 16-ft wall.

Happily, this is a straightforward calculation.

The wall extension is 16 ft wide, less the stud widths. We already have these calculated in Table 4:

When 11 studs are used (16 in. stud spacing), the width is 13.83 ft
When 10 studs are used (18 in. stud spacing), the width is 14 ft
When 9 studs are used (20 in. and 22 in. stud spacing), the width is 14.17 ft
When 8 studs are used (24 in. stud spacing), the width is 14.33 ft

The height is equal to the rise (A), which is 1.76 ft.

So, the total wall extension area requiring insulation coverage is:

	Area
11 studs; 16 in. stud spacing	1.76 ft x 13.83 ft = 24.34 ft²
10 studs; 18 in. stud spacing	1.76 ft x 14 ft = 24.64 ft²
9 studs; 20 in. and 22 in. stud spacing	1.76 ft x 14.17 ft = 24.94 ft²
8 studs; 24 in. stud spacing	1.76 ft x 14.33 ft = 25.22 ft²

Table 10

Total Skillion Roof Area and New Wall Area

For ease, we will incorporate the wall extension area into the total wall area instead of the total roof area. Below is an extension of Table 6.

Stud spacing	2×4 studs	2×6 studs	2×8 studs
16 in.	349.34 ft² + 24.34 ft² = 373.68 ft²	344 ft² + 24.34 ft² = 368.34 ft²	338.68 ft² + 24.34 ft² = 363.02 ft²
18 in.	352 ft² + 24.64 ft² = 376.64 ft²	349.34 ft² + 24.64 ft² = 373.98 ft²	344 ft² + 24.64 ft² = 368.64 ft²
20 in.	357.32 ft² + 24.94 ft² = 382.26 ft²	352 ft² + 24.94 ft² = 376.94 ft²	346.66 ft² + 24.94 ft² = 371.6 ft²
22 in.	357.32 ft² + 24.94 ft² = 382.26 ft²	352 ft² + 24.94 ft² = 376.94 ft²	346.66 ft² + 24.94 ft² = 371.6 ft²
24 in.	360 ft² + 25.22 ft² = 385.22 ft²	354.68 ft² + 25.22 ft² = 379.9 ft²	349.34 ft² + 25.22 ft² = 374.56 ft²

Table 11

Now for the total skillion roof area for 10×16 shed:

	Roof panel area	Gable space area	Total roof area
2×4	140.37 ft²	6.74 ft²	147.11 ft²
2×6	140.37 ft²	3.28 ft²	143.65 ft²

Table 12

These calculations can be used to work out the amount of insulation required for sheds of different sizes, like 10×12.

Amount of Insulation Required to Insulate 10×16 Shed

Flat Roof

2×4 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	349.34 ft²	138.33 ft²	487.67 ft²
18 in.	352 ft²	138.33 ft²	490.33 ft²
20 in.	357.32 ft²	138.33 ft²	495.65 ft²
22 in.	357.32 ft²	138.33 ft²	495.65 ft²
24 in.	360 ft²	138.33 ft²	498.33 ft²

Table 13

2×6 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	344 ft²	138.33 ft²	482.33 ft²
18 in.	349.34 ft²	138.33 ft²	487.67 ft²
20 in.	352 ft²	138.33 ft²	490.33 ft²
22 in.	352 ft²	138.33 ft²	490.33 ft²
24 in.	354.68 ft²	138.33 ft²	493.01 ft²

Table 14

2×8 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	338.68 ft²	138.33 ft²	477.01 ft²
18 in.	344 ft²	138.33 ft²	482.33 ft²
20 in.	346.66 ft²	138.33 ft²	484.99 ft²
22 in.	346.66 ft²	138.33 ft²	484.99 ft²
24 in.	349.34 ft²	138.33 ft²	487.67 ft²

Table 15

Gable Roof

2×4 Rafters and 2×4 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	349.34 ft²	151.42 ft²	500.76 ft²
18 in.	352 ft²	151.42 ft²	503.42 ft²
20 in.	357.32 ft²	151.42 ft²	508.74 ft²
22 in.	357.32 ft²	151.42 ft²	508.74 ft²
24 in.	360 ft²	151.42 ft²	511.42 ft²

Table 16

2×4 Rafters and 2×6 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	344 ft²	151.42 ft²	495.42 ft²
18 in.	349.34 ft²	151.42 ft²	500.76 ft²
20 in.	352 ft²	151.42 ft²	503.42 ft²
22 in.	352 ft²	151.42 ft²	503.42 ft²
24 in.	354.68 ft²	151.42 ft²	506.1 ft²

Table 17

2×4 Rafters and 2×8 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	338.68 ft²	151.42 ft²	490.01 ft²
18 in.	344 ft²	151.42 ft²	495.42 ft²
20 in.	346.66 ft²	151.42 ft²	498.08 ft²
22 in.	346.66 ft²	151.42 ft²	498.08 ft²
24 in.	349.34 ft²	151.42 ft²	500.76 ft²

Table 18

2×6 Rafters and 2×4 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	349.34 ft²	148.1 ft²	497.44 ft²
18 in.	352 ft²	148.1 ft²	500.1 ft²
20 in.	357.32 ft²	148.1 ft²	505.52 ft²
22 in.	357.32 ft²	148.1 ft²	505.52 ft²
24 in.	360 ft²	148.1 ft²	508.1 ft²

Table 19

2×6 Rafters and 2×6 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	344 ft²	148.1 ft²	492.1 ft²
18 in.	349.34 ft²	148.1 ft²	497.44 ft²
20 in.	352 ft²	148.1 ft²	500.1 ft²
22 in.	352 ft²	148.1 ft²	500.1 ft²
24 in.	354.68 ft²	148.1 ft²	502.48 ft²

Table 20

2×6 Rafters and 2×8 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	338.68 ft²	148.1 ft²	486.78 ft²
18 in.	344 ft²	148.1 ft²	492.1 ft²
20 in.	346.66 ft²	148.1 ft²	494.76 ft²
22 in.	346.66 ft²	148.1 ft²	494.76 ft²
24 in.	349.34 ft²	148.1 ft²	497.44 ft²

Table 21

Skillion Roof

2×4 Rafters and 2×4 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	373.68 ft²	147.11 ft²	520.79 ft²
18 in.	376.64 ft²	147.11 ft²	523.75 ft²
20 in.	382.26 ft²	147.11 ft²	529.37 ft²
22 in.	382.26 ft²	147.11 ft²	529.37 ft²
24 in.	385.26 ft²	147.11 ft²	532.37 ft²

Table 22

2×4 Rafters and 2×6 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	368.34 ft²	147.11 ft²	515.45 ft²
18 in.	373.98 ft²	147.11 ft²	521.09 ft²
20 in.	376.94 ft²	147.11 ft²	524.05 ft²
22 in.	376.94 ft²	147.11 ft²	524.05 ft²
24 in.	379.9 ft²	147.11 ft²	527.01 ft²

Table 23

2×4 Rafters and 2×8 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	363.02 ft²	147.11 ft²	510.13 ft²
18 in.	368.64 ft²	147.11 ft²	515.75 ft²
20 in.	371.6 ft²	147.11 ft²	518.71 ft²
22 in.	371.6 ft²	147.11 ft²	518.71 ft²
24 in.	374.56 ft²	147.11 ft²	521.67 ft²

Table 24

2×6 Rafters and 2×4 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	373.68 ft²	143.65 ft²	517.33 ft²
18 in.	376.64 ft²	143.65 ft²	520.29 ft²
20 in.	382.26 ft²	143.65 ft²	525.91 ft²
22 in.	382.26 ft²	143.65 ft²	525.91 ft²
24 in.	385.26 ft²	143.65 ft²	528.91 ft²

Table 25

2×6 Rafters and 2×6 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	368.34 ft²	143.65 ft²	511.99 ft²
18 in.	373.98 ft²	143.65 ft²	517.63 ft²
20 in.	376.94 ft²	143.65 ft²	520.59 ft²
22 in.	376.94 ft²	143.65 ft²	520.59 ft²
24 in.	379.9 ft²	143.65 ft²	523.55 ft²

Table 26

2×6 Rafters and 2×8 Studs

Stud spacing	Wall area	Roof area	Total area
16 in.	363.02 ft²	143.65 ft²	506.67 ft²
18 in.	368.64 ft²	143.65 ft²	512.29 ft²
20 in.	371.6 ft²	143.65 ft²	515.25 ft²
22 in.	371.6 ft²	143.65 ft²	515.25 ft²
24 in.	374.56 ft²	143.65 ft²	518.21 ft²

Table 27

If you are insulating a shed, you should also consider ventilating it. There are a number of ways to achieve this.